5213. Обратные
Дано простое число n. Обратным к числу i (1 ≤ i < n) называется такое j, что i * j = 1 (mod n). Можно доказать, что для каждого i существует единственное обратное.
Для всех допустимых i найдите обратные к ним числа.
Вход. Одно простое число n (2 ≤ n ≤ 106).
Выход. Выведите n – 1 число. i-ым следует
вывести число, обратное к i.
|
Пример
входа |
Пример
выхода |
|
5 |
1 3 2 4 |
РЕШЕНИЕ
возведение
в степень
Анализ алгоритма
Поскольку число n простое, то по теореме Ферма
in-1 mod n = 1 для всякого 1 ≤ i < n. Равенство можно переписать в виде (i * in-2)
mod n = 1, откуда обратным числом к i является j = in-2
mod n.
Обратное число
можно найти используя расширенный алгоритм Евклида. Пусть следует
решить сравнение: ax = 1 (mod n). Рассмотрим уравнение
ax + ny = 1
и найдем его
частичное решение (x0, y0) при помощи
расширенного алгоритма Евклида. Возьмем уравнение ax0 + ny0 = 1 по модулю n, получим ax0 = 1 (mod n). В случае
отрицательного значения x0, к нему следует
прибавить n. Таким образом x0 = a-1 (mod n) является
обратным к a.
В обоих
алгоритмах для каждого i (1 ≤ i < n) мы искали обратное за время O(log2n). Таким образом работа всего алгоритма
составит O(n
log2n).
Рассмотрим
решение за O(n).
Теорема. Если inv[i] – число, обратное i по модулю n, то
inv[i] = 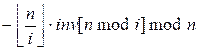
Доказательство. Известно, что 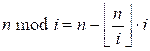
Возьмем по
модулю n обе стороны: 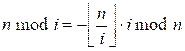
Домножим обе
стороны на i-1 * (n mod i) -1:
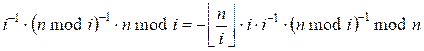
После упрощения
получим:

Согласно
формуле, приведенной в теореме, значение inv[i] для каждого i (1 ≤ i < n) может быть найдено за время O(1). Таким образом
все обратные элементы будут найдены за O(n).
Пример
Пусть n = 5. Построим таблицу:
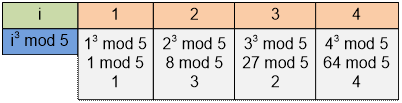
Найдем обратные элементы по формуле из
теоремы:
inv[1] = 1 (базовый случай)
inv[2] =  = (-2 ∙ inv[1]) mod 5 = -2 mod
5 = 3
= (-2 ∙ inv[1]) mod 5 = -2 mod
5 = 3
inv[3] =  = (-1 ∙ inv[2]) mod 5 = -3 mod 5 = 2
= (-1 ∙ inv[2]) mod 5 = -3 mod 5 = 2
inv[4] =  = (-1 ∙ inv[1]) mod 5 = -1 mod 5 = 4
= (-1 ∙ inv[1]) mod 5 = -1 mod 5 = 4
Реализация алгоритма
Функция Pow возвращает значение xn
mod m.
long long
Pow(long long
x, long long n,
long long m)
{
if (n == 0) return 1;
if (n % 2 ==
0) return Pow((x * x) % m, n / 2, m);
return (x *
Pow(x, n - 1, m)) % m;
}
Основная часть программы. Читаем входное значение n.
scanf("%d",&n);
Для каждого значения i выводим обратное к нему число in-2 mod n.
for(i = 1; i < n; i++)
printf("%lld
",Pow(i,n-2,n));
printf("\n");
Реализация алгоритма –
расширенный алгоритм Евклида
#include <stdio.h>
int n, i, d, x, y;
void gcdext(int a, int b, int &d, int &x, int &y)
{
if (b == 0)
{
d = a; x
= 1; y = 0;
return;
}
gcdext(b,
a % b, d, x, y);
int s = y;
y = x -
(a / b) * y;
x = s;
}
int main(void)
{
scanf("%d", &n);
for (i = 1; i < n; i++)
{
// i * x
+ n * y = 1
gcdext(i,
n, d, x, y);
if (x < 0) x += n;
printf("%d ", x);
}
printf("\n");
return 0;
}
Реализация алгоритма – линейное
решение
Объявим массив inv, в
котором будем вычислять обратные элементы:
inv[i]
= i-1 mod n.
#define MAX 1000001
int inv[MAX];
Читаем входное значение n.
scanf("%d", &n);
Вычисляем обатные элементы согласно
формуле.
inv[1] = 1;
for (i = 2; i <= n; i++)
inv[i] = n - 1LL * (n / i) * inv[n % i] % n;
Выводим ответ.
for (i = 1; i < n; i++)
printf("%d ", inv[i]);
Java реализация
import java.util.*;
public class Main
{
static long PowMod(long x, long n, long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
long n = con.nextLong();
for(int i = 1; i < n; i++)
System.out.print(PowMod(i,n-2,n) + " ");
System.out.println();
con.close();
}
}
Java реализация
– линейное решение
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int inv[] = new int[n];
inv[1] = 1;
for (int i = 2; i < n; i++)
inv[i] = (int) (n - 1L * (n / i) * inv[n % i] % n);
for(int i = 1; i < n; i++)
System.out.print(inv[i] + " ");
System.out.println();
con.close();
}
}
Python реализация – линейное решение
n = int(input())
inv = [0 for _ in range(n + 1)]
inv[1] = 1;
for i in range(2,n):
inv[i] = n - (n // i) * inv[n % i] % n;
for i in range(1,n):
print(inv[i], end= " ")